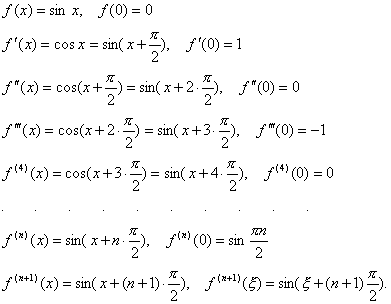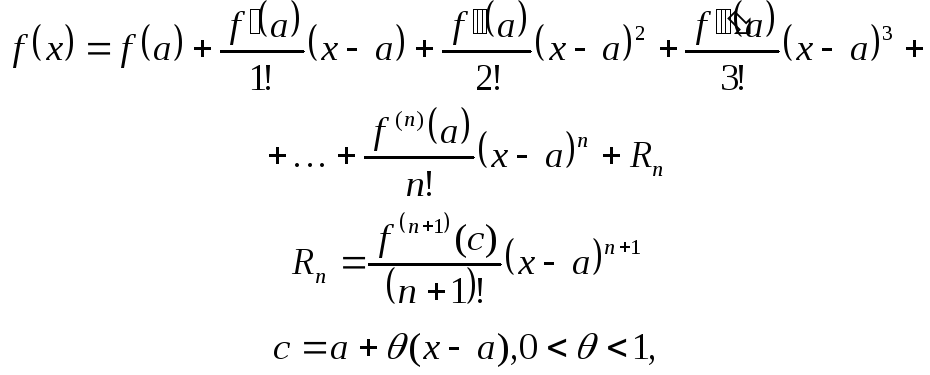
Формула Тейлора
Пусть функция f x определена в некоторой окрестности точки x0 и n раз дифференцируема в точке x0. Они уточняют формулу 1. Теорема 1 Пеано.





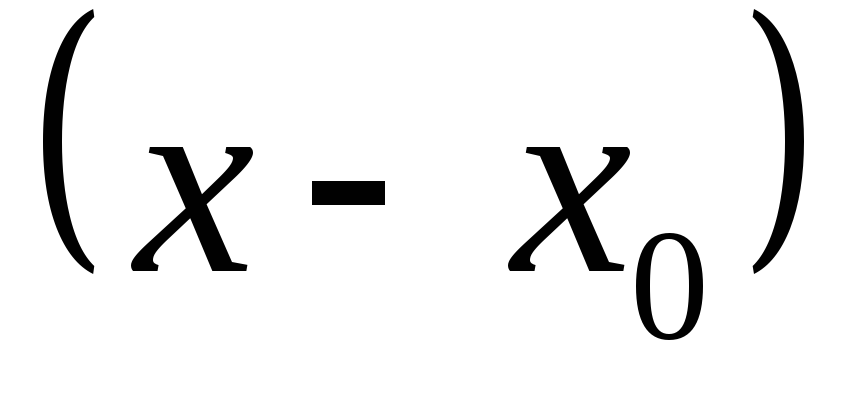




Помочь проекту. Тогда в некоторой окрестности можно написать равенство. Пусть в. Тогда в. Пусть , непрерывна на отрезке , на интервале. Тогда справедлива формула 1 , в которой.
- Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля.
- Перейти к основному содержанию. Вы используете гостевой доступ Вход.
- Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде.
- Даем определения производной и дифференциала.
- Конев В.
- Помочь проекту. Остаточный член в формуле Тейлора.









В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями. Верный ответ. Неверный ответ.